O M P U

Der neue Schlüssel

- eine Harmonielehre -

2. Die Quinte

Der im ersten Kapitel beschriebene Versuch mit der halbierten schwingenden Saite stammt von Pythagoras aus dem sechsten Jahrhundert vor unserer Zeitrechnung. Beim Teilen der Saite im Verhältnis 1:2 erklingt ein neuer Ton: Die Quinte.

Nehme ich beispielsweise bei einer Gitarre den Ton A und teile die Saite im Verhältnis 1:2, indem ich den Finger über dem Ende des siebten Bundes auf die Saite lege, höre ich den Ton e.

Diese enge Verwandtschaft zwischen dem Grundton und seiner Quinte ist also nicht von Menschen erfunden, sondern eine Vorgabe der Natur, die man jederzeit mit diesem Experiment überprüfen kann.
 
Was wäre naheliegender, als zu untersuchen, welcher Ton klingt, wenn ich aus meinem neu gefundenen Ton wiederum die Quinte hervorlocke? Dazu teile ich eine auf e gestimmte Saite im Verhältnis ein Drittel zu zwei Drittel. Die Quinte des Tons e ist der Ton h, die Quinte von h ist ges. Setze ich dieses Spiel konsequent fort, lande ich nach zwölf Tönen wieder beim Ausgangston.

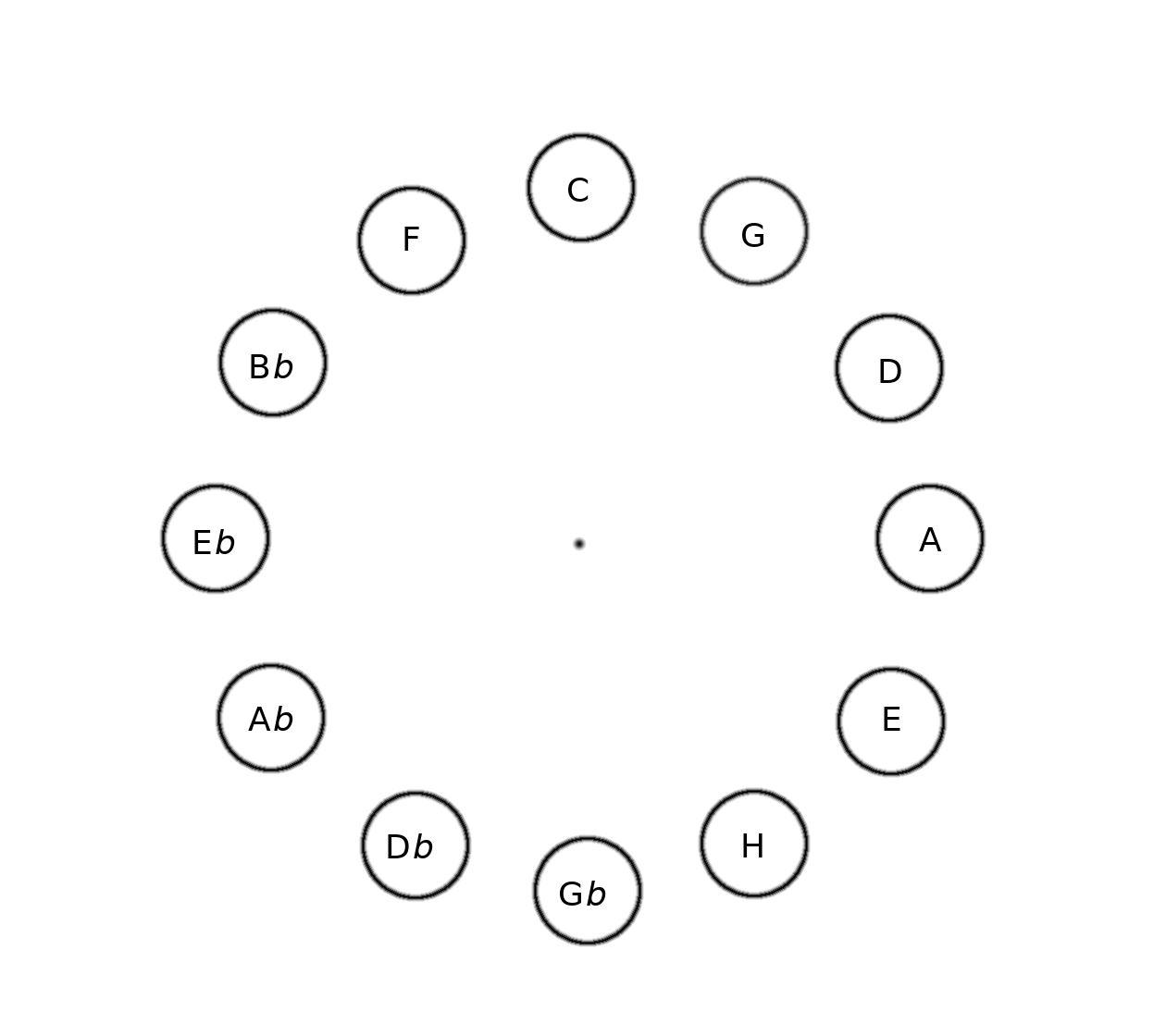
Die Zahl zwölf begegnet uns ja häufig, vertraut in der Einteilung der Stunden des Tages. Ordne ich die Reihe meiner gefundenen Quinten wie die Stunden auf einer Uhr, erhalte ich den Quintenzirkel: Eine Stunde weiter bedeutet hier eine Quinte weiter.
Der oben beschriebene Weg des Kammertons A verlief von drei bis sechs Uhr.

Um die Wanderung durch den Quintenzirkel einfacher zu machen, hier eine kleine Bastelaufgabe: Druckt die folgende Grafik aus und schneidet erst einen Kreis aus, dann seinen Nachbarn, dann zwei Nachbarn...
Wenn man das Blatt mit einer Heftzwecke auf den Quintenzirkel fixiert und dreht, sieht man die zu spielenden Töne.

Praxisteil

Harmonielehre macht nur im Zusammenhang mit Musik Sinn, und zwar mit gespielter Musik.
Daher jetzt ein kleiner Praxisteil: Spielt und experimentiert mit zwei, drei und vier benachbarten Quinten. Wie oft dabei ein Quintenpaar auftaucht, wie schnell oder mit welchem Rhythmus soll erstmal nicht festgelegt werden.

Hier meine Versuche:

Quintus mit zwei Nachbartönen im Quintenzirkel

Quintus III. mit drei Nachbartönen im Quintenzirkel

Quintus IV. mit vier Nachbartönen im Quintenzirkel

Kontakt